우주선의 방향과 속도를 조절하는 ‘중력도움 항법’(상)

그림 1. 태양탐사선 파커(Parker)와 수성탐사선 베피콜롬보(BepiColombo) 출처: NASA, ESA

[윤복원의 물리상식으로 푸는 요즘 세상]
로켓 추진력만으론 심우주 항해에 한계
적절한 거리서 행성 중력 이용하는 원리

그림 1. 태양탐사선 파커(Parker)와 수성탐사선 베피콜롬보(BepiColombo) 출처: NASA, ESA

2018년에 발사된 태양탐사선 ‘파커’(Parker)와 수성탐사선 ‘베피콜롬보‘(BepiColombo)는 탐사 목적뿐만 아니라 목표한 천체에 어떻게 다가가는지 주목할 필요가 있다. 두 탐사선 모두 비교적 가까운 천체인 태양과 수성을 탐사함에도 약 7년 동안 긴 항해를 한다. 그 사이 탐사선은 금성 또는 수성에 여러번 접근해 방향과 속도를 조절한다. 이 과정을 통해 탐사선은 목표한 궤도에 조금씩 다가간다. 이렇게 행성에 접근해 지나가면서 우주선의 방향과 속도를 조절하는 항법을 ‘중력도움’(gravity assist)이라고 한다.

‘스윙바이’(swing-by) 또는 ‘슬링샷’(slingshot)이라고도 불리는 ‘중력도움’은 로켓 추진을 사용하지 않고도 우주선의 속도를 높일 수 있는 항법으로 잘 알려져 있다. 수백kg 이상의 장비를 지닌 우주선을 로켓 추진만으로 토성 또는 그보다 멀리 있는 천체에 보내는 것은 매우 어렵다. 대신 행성에 접근해 지나가는 중력도움 항법으로 태양의 중력을 완전히 벗어나고도 남을 만큼의 속도를 추가로 얻는다.

태양이나 태양에 가장 가까운 행성인 수성을 탐사할 때는 오히려 우주선의 빠른 속도가 문제가 된다. 방향 전환이나 감속을 해야 하는데 우주선의 빠른 속도 때문에 이것이 쉽지 않기 때문이다. 태양탐사선 ‘파커’와 수성탐사선 ‘베피콜롬보’는 이 문제를 중력도움 항법으로 해결한다. 때로는 우주선의 속도를 높이거나 줄이고, 방향을 바꾸는 데 사용하는 중력도움 항법의 원리가 무엇인지 좀 더 구체적으로 살펴보자.

지구에서 발사한 우주선은 초속 29.8km의 속도를 덤으로 얻는다

태양은 태양계 전체 질량의 99.8% 이상을 차지한다. 지구 질량보다 33만배 크고, 태양에서 가장 큰 행성인 목성의 질량보다도 1000배 이상 크다. 태양이 끌어당기는 중력도 매우 커서, 태양 표면에서의 중력은 지구 표면 중력의 28배에 이른다. 이런 태양의 중력이 구심력으로 작용해 태양계 나머지 천체들이 태양 주위를 돈다. ‘공전’이라고 부르는 천체의 움직임이다. 태양에서 약 1억5천만km 떨어져 있는 지구는 태양 주위를 1년에 1바퀴씩 돈다. 이로부터 계산한 지구의 평균 공전속도는 초속 29.8km(시속 10만7천km) 정도다.[1] 대륙 사이를 비행하는 대형 여객기의 속도보다 100배 이상 빠른 속도다.

지구 위에 있는 것은 모두 공전하는 지구와 함께 같이 움직인다. 지구 위에 가만히 서 있는 사람 본인은 움직이지 않는 것처럼 느낀다. 하지만 지구가 공전하는 것을 볼 수 있는 위치, 예를 들면 태양에서 본다고 가정하면 지구에 가만히 서 있는 사람도 지구가 움직이는 것과 같이 움직인다. 지구에서 발사하는 우주선도 마찬가지로 지구와 같이 움직이므로 지구의 공전속도를 기본으로 지닌다.[2] 지구의 중력을 뿌리치고 지구 공전 방향으로 멀어지는 우주선의 경우, 지구에서 보는 우주선의 속도는 우주선이 지구에서 멀어지는 속도지만, 태양에서 보면 우주선의 속도는 지구의 공전속도가 더해진 속도다.[3] 지구의 공전속도를 덤으로 얻는다는 얘기다.

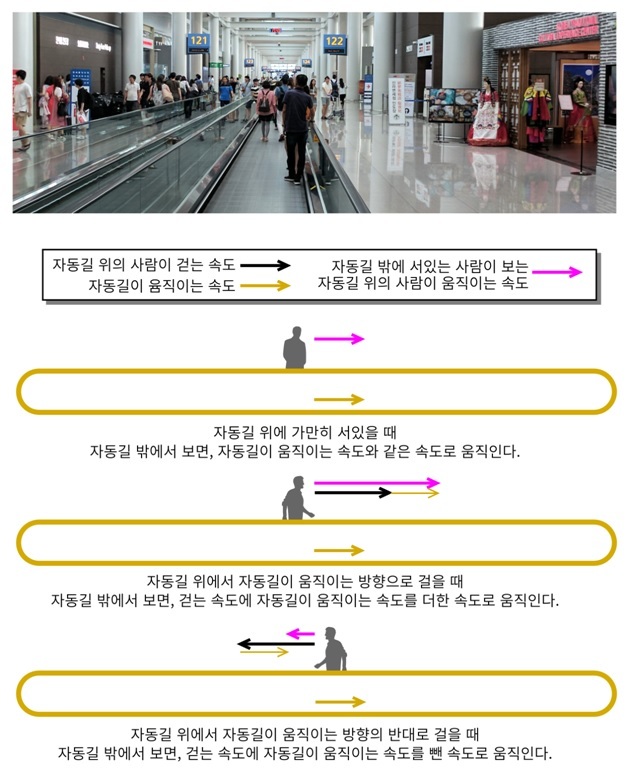
공항에 있는 ‘자동길'이라고 부르는 움직이는 길을 생각해보자. 자동길 위에 가만히 서 있는 사람이 옆에서 똑같이 서 있는 사람을 보면 그 사람은 상대적으로 움직이지 않는 것으로 보인다. 하지만 자동길 위에 있지 않고 자동길 밖의 건물 바닥에 서 있는 사람이 보면, 이 사람은 자동길이 움직이는 속도로 움직인다. 이번에는 자동길 위에서 자동길이 움직이는 방향으로 걷는 사람이 있다고 하자. 자동길 위에 서 있는 사람에게 이 사람은 걷는 속도로 움직인다. 하지만 자동길 밖에 서 있는 사람이 보기에 이 사람은 걷는 속도에 자동길이 움직이는 속도까지 더해져 훨씬 빠르게 움직이는 것으로 보인다. 자동길에서 걷는 사람은 자동길이 움직이는 속도를 덤으로 얻는 셈이다. 자동길에 서 있는 사람을 지구에 서있는 사람, 자동길에서 걷는 사람을 지구를 떠나는 우주선, 건물 바닥에 서 있는 사람을 태양에서 보는 사람이라고 생각하면 우주선이 지구의 공전속도를 덤으로 얻는 것을 좀 더 쉽게 이해할 수 있다.

그림 2. 상대속도를 이해하는 데 좋은 예인 자동길(움직이는 길). 맨위 사진: 인천공항의 자동길, 사진 밑의 첫번째 그림: 움직이는 자동길에 서 있는 사람 본인은 자동길 위에서 움직이지 않고 가만히 서 있지만, 건물 바닥에 서 있는 사람이 보기에는 이 사람은 자동길이 움직이는 속도와 같은 속도로 움직인다. 가운데 그림: 자동길에서 자동길이 움직이는 방향으로 걷는 사람의 경우 자동길에 서 있는 사람이 보면 걷는 속도로 움직이지만, 건물 바닥에 서 있는 사람이 보면 걷는 속도에 자동길이 움직이는 속도가 더해져 더 빨리 움직인다. 맨아래 그림: 만약에 자동길이 움직이는 방향과 반대방향으로 걷는 사람을 건물 바닥에 서 있는 사람이 보면 오히려 더 느리게 움직이는 것으로 보인다. (사진 출처: Wikimedia Commons, 그림 일부 출처: openclipart.org)

태양중력 탈출속도: 태양의 중력을 벗어나는 데 필요한 최소 속도

속도가 빠를수록 우주선은 움직이는 관성만으로 태양의 중력을 뿌리치고 태양에서 더 멀리 멀어질 수 있다. 공을 위로 던질 때 빠르게 던질수록 지구의 중력을 뿌리치고 더 높이 올라가는 것과 같은 원리다. 우주선의 속도가 충분히 크면 태양의 중력을 완전히 뿌리치고 태양계를 벗어날 수도 있다. 이렇게 태양의 중력을 완전히 뿌리칠 수 있는 최소한의 속도를 태양 중력 ‘탈출속도’라고 부른다. 태양 중력 ‘탈출속도’는 중력을 만드는 태양의 위치에서 본 속도를 말한다. 태양에서 지구만큼 떨어진 거리에서는 초속 42.1km가 태양 중력 탈출속도다. 지구의 공전 속도보다 1.414(=√2)배 더 큰 속도다.[4] 태양에서 1억5천만km 떨어진 곳에서 공을 초속 42.1km로 던지면, 그 공은 움직이는 관성만으로 태양의 중력을 완전히 벗어나 명왕성을 넘어 아주 멀리 갈 수 있다는 얘기다. 그런데, 지구에서 출발한 우주선은 이미 지구 공전속도를 덤으로 얻고 가기 때문에, 태양계를 벗어나기 위해 로켓 추진으로 가속할 속도는 그만큼 줄어든다.

그러나 아쉽게도 지구에서 발사된 우주선이 태양 중력 탈출속도와 공전속도의 차이인 초속 12.3km(초속 42.1km에서 초속 29.8km를 뺀 것)만으로는 태양계를 완전히 벗어날 수 없다. 지구의 중력도 벗어나야 하기 때문이다. 지구에서 출발해 태양계를 벗어나려면, 우주선은 ‘제3 우주속도’라고 불리는 초속 16.7km로 지구에서 멀어져야 한다.[5] 그런데 ‘제3 우주속도’는 지구에서 출발한 우주선이 태양계를 벗어나기 위한 최소한의 속도이기 문에, 이 속도로 시작해서 태양계의 언저리나 그 너머의 아주 먼 곳에 가려면 시간이 매우 오래 걸린다. 빨리 목적지에 도착하려면 더 빠른 속도가 필요하다. 로켓 추진만으로 이런 속도를 내기는 어렵고, 중력도움 항법으로 속도를 높여 부족한 속도를 채운다.

중력도움 항법으로 우주선의 속도를 높이는 원리

행성의 중력을 이용하는 중력도움 항법을 시행할 때 우주선은 행성에 다가갔다 멀어지는 과정을 거친다.[6] 이 과정을 통해 우주선의 어떻게 속도를 높일 수 있는지를 이해하는 데는 다음 두 가지 사실이 중요하다. 첫째는 행성은 태양 주위를 공전한다는 것이고, 둘째는 어떤 위치에서 보느냐에 따라 우주선의 속도는 다르다는 것이다. 비록 ‘중력도움 항법’이라는 이름에는 행성의 공전이라는 내용이 겉으로 드러나 있지 않지만, 중력도움 항법으로 우주선의 속도를 조절하는 데는 행성의 중력뿐만 아니라 행성의 공전도 이용한다.

태양의 중력을 벗어나는 우주선의 경우, 태양에서 보는 우주선의 속도를 따져야 한다. 하지만 속도를 높이는 중력도움항법을 태양에서 보는 속도만으로 이해하는 것은 그리 간단하지 않다. 하지만 행성의 위치에서 보는 우주선의 속도를 먼저 따지고 나중에 행성의 공전속도를 영향을 헤아리면, 비교적 어렵지 않게 태양에서 보는 우주선의 속도 변화를 이해할 수 있다.

먼저 행성의 위치에서 보는 우주선의 속도를 따져 보자. 이 기준에서는 우주선이 행성에 다가갈 때나 멀어질 때나 행성에서 떨어진 거리만 같다면 우주선 속도의 크기는 같다. 이는 에너지 보존의 법칙을 적용해서 이해할 수 있다. 행성에서 떨어진 거리가 같으면 위치에너지가 같다. 이 상황에서 위치에너지와 운동에너지를 더한 전체 에너지가 보존되려면 운동에너지가 같아야 하고 결국 속도의 크기가 같아야 한다. 다가가고 멀어지는 방향만 달라질 뿐이다.

그림 3. 행성의 중심에서 본다고 가정했을 때 행성에 다가왔다가 멀어지는 우주선의 속도. 행성에서의 거리가 같으면 우주선이 움직이는 방향만 다를 뿐 속도의 크기는 같다.

반면 태양의 위치에서 보는 우주선의 속도는, 행성에서 보는 우주선의 속도에 행성의 공전속도가 더해진 속도다. 만약에 우주선이 행성의 공전방향으로 멀어진다면 우주선의 속도 크기에 행성의 공전 속도의 크기를 더해주기만 하면 된다. 하지만 대부분의 경우 우주선이 움직이는 방향이 행성의 공전방향과 같지 않기 때문에 단순히 속도 크기만 더하는 것이 아닌 방향까지 고려하는 ‘벡터 더하기’ 방식으로 더한다. 행성의 위치에서 볼 때 행성에서 떨어진 거리만 같으면 다가갈 때나 멀어질 때 크기가 같았던 우주선의 속도가, 태양의 위치에서 볼 때는 행성의 공전속도가 더해지면서 많은 경우 그 크기가 달라진다. <그림 2>에서 처럼 움직이는 자동길에 가만히 앉아 있는 사람에게는 자동길에서 똑같은 속도로 걷는 사람이 어느 방향으로 걸어도 속도의 크기는 같다. 하지만 건물 바닥에 있는 사람이 볼때는 자동길이 움직이는 방향으로 걸어가는 사람이 반대방향으로 걷는 사람보다 더 빠른 것과 비교할 수 있다.

중력도움 항법을 속도를 높이는 목적으로 사용하려면, 태양에서 볼 때 행성에서 멀어지는 속도가 커지도록 접근하고 멀어져야 한다. 가장 이상적인 방법은 행성이 공전하는 방향과 반대방향으로 접근해서 행성이 공전하는 방향과 같은 방향으로 움직이는 것이다. 그러면 <그림 2>의 자동길에서 걷는 사람을 자동길 밖에 서 있는 사람이 볼때, 자동길이 움직이는 반대방향으로 걷는 사람은 느리게 움직이지만 이 사람이 방향을 바꿔 자동길이 움직이는 방향으로 걸으면 빠르게 움직이는 상황과 비슷하다. 걷는 사람은 똑같은 속도로 방향만 바꿔서 걷지만 자동길 밖에서 보면 자동길 방향으로 걷는 사람이 훨씬 빠르다. 이런 이상적인 중력도움 항법을 시행하면 행성 공전속도의 두배에 해당하는 속도를 추가로 얻는다.

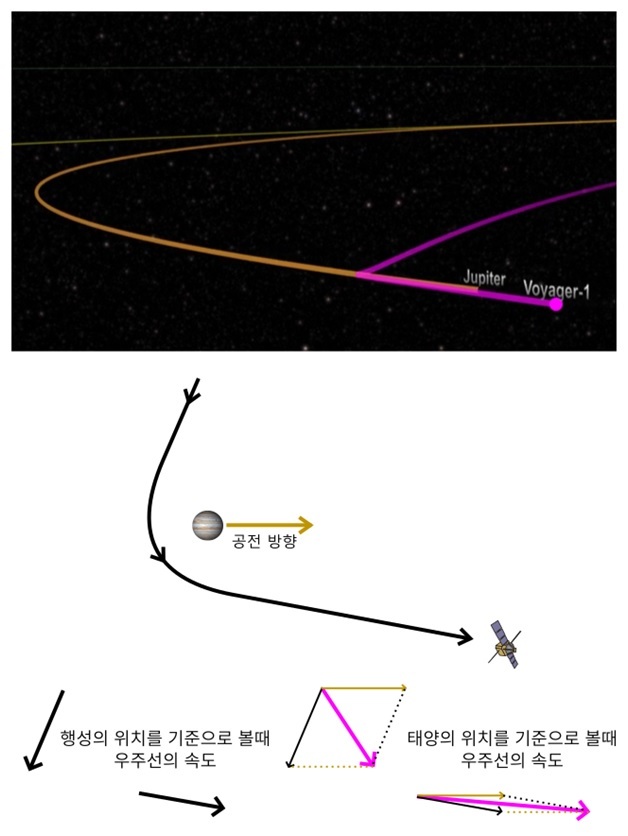
실제로 우주선이 항해할 때는 행성이 공전하는 반대방향으로 접근하지 않는다. <그림 4>에서와 같이 행성이 공전하는 방향과 많이 다르게 접근해서 비슷하게 멀어진다. 이 경우에도 멀어질 때 우주선의 속도가 다가갈 때보다 크다. 이러한 방식으로 목성에 접근해 중력도움 항법을 시행하면 높일 수 있는 우주선의 속도는 초속 10km 이상이다. 로켓 추진만으로 이 만큼 속도를 높이려면 상당한 로켓연료가 필요하고, 이를 우주에 올려놓기 위한 발사체 크기도 훨씬 커져야 한다. 중력도움 항법을 시행하면, 그만큼 발사체 크기와 연료를 줄일 수 있어 훨씬 경제적이고 효율적이다.

그림 4. 중력도움 항법으로 속도를 높이는 방법: (맨 위 그림) 목성을 지나갈 때 보이저 1호의 궤적 (출처: NASA JPL). (가운데 그림) 중력도움 항법으로 속도를 높일 때 행성의 위치에서 본 전형적인 우주선의 궤적. 우주선이 행성에 접근하는 방향은 행성이 공전하는 방향과 다르고, 우주선이 멀어지는 방향은 행성이 공전하는 방향과 비슷하다. (맨 아래 그림) 행성의 위치에서 본 우주선의 속도(왼쪽의 검은색 화살표)는 다가갈 때나 멀어질 때나 같다. 반면 태양의 위치에서 본 우주선의 속도(오른쪽의 핑크색 화살표)는 행성의 공전속도가 더해져서 멀어질 때가 더 크다. 두 경우 모두 행성에서의 거리가 같을 때의 속도를 비교했을 경우다. 공전속도를 더할 때는 단순 크기만 더하는 것이 아닌, 방향까지 고려한 벡터 더하기를 한다.

행성이 공전하는 방향과 비슷하게 멀어지기 위해서는 우주선이 행성에 접근하는 거리를 조절하는 것이 중요하다. 만약에 행성에 너무 가까이 접근하면, 우주선이 행성 중력의 영향을 너무 많이 받아서 우주선이 날아가는 방향이 너무 많이 꺾일 수 있다. 이런 경우 오히려 우주선의 속도가 더 느려지거나 아예 행성의 중력에 갇혀 행성 주위를 영원히 도는 인공위성이 될 수도 있다. 반면 너무 멀리 접근하면 행성 중력의 영향을 너무 적게 받아서 우주선이 방향이 충분히 꺾이지 않을 수 있다. 그만큼 우주선 속도를 높이는 효과도 작아진다.

공전하는 행성의 중력을 이용해 우주선의 속도를 높이는 중력도움 항법은 1961년에 제트추진연구소(JPL: Jet Propulsion Laboratory)에 인턴으로 일하던 미노비치(Michael A. Minovitch)가 찾아낸 것으로 알려졌다.[7] 1972년 3월3일에 발사된 파이오니어 10호(Pioneer 10)가 중력도움 항법으로 태양계를 벗어날 수 있는 속도에 도달한 최초의 탐사선이다. 발사한 지 1년 9개월이 지난 1973년 12월에 목성에 접근하는 중력도움 항법으로 초속 12km이상의 속도를 추가로 높였다. 목성 너머의 우주를 탐사하는 다른 우주선들도 모두 이 항법을 이용해 속도를 높였다.[8] 파이오니어 11호, 보이저 1호와 2호, 토성탐사선 ‘카시니-하위헌스’, 명왕성을 탐사한 ‘뉴 호라이즌스’가 대표적인 경우들이다.

----------------------------------

카시니-하위헌스(Cassini-Huygens)호

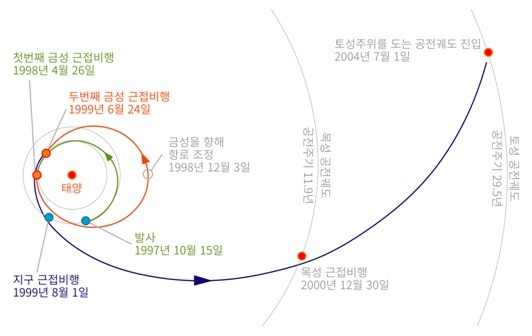
토성 탐사선인 ‘카시니’와 토성의 위성 타이탄 착륙선인 ‘하위헌스’로 구성된 ‘카시니-하위헌스’호는 탐사선 질량만 2.5톤에 이르러 보이저 1호나 2호보다 3배 이상 컸다. 당시 로켓기술로는 이만한 질량의 탐사선을 토성까지 직접 보낼 만한 속력을 내기 어려웠다. 대신 ‘카시니-하위헌스’호는 중력도움 항법을 네번이나 시행해 토성까지 갈 수 있는 속도로 높였다. 처음 두번은 금성에, 세번째는 지구에, 그리고 마지막은 목성에 가까이 다가가는 중력도움 항법이었다.

카시니-하위헌스호의 비행 궤적 : 금성에서 두번, 지구에서 한번 목성에서 한번, 총 네번의 중력도움 항법으로 탐사선의 속도를 높여서, 2.5톤에 이르는 탐사선이 토성에 도달할 수 있었다. (원본 그림 출처: NASA)

‘하위헌스’ 착륙선은 2005년 1월에 타이탄에 진입한다. 남은 ‘카시니’ 토성 탐사선은 2017년까지 토성과 토성의 위성들을 탐사하다가, 2017년 9월 11일에 토성의 가장 큰 달인 ‘타이탄’을 근접비행하면서 비행 방향을 바꿔 4일 후인 9월 15일 토성에 충돌해 최후를 맞았다.

---------------------------------------

*(하)편 보기

윤복원/미국 조지아공대 연구원(전산재료과학센터·물리학) [e-mail]

<주>

[1] 태양도 은하계 중심을 기준으로 보면 초속 230km로 움직인다. 태양계 안에서 주로 탐사활동을 하는 우리로서는 태양의 위치를 기준으로 한 속도로 계산하는 것이 여러모로 편리하다.

[2] 지구 자전으로 인해 움직임도 있다. 적도 지역에서는 자전속도가 초속 0.46km(=460m) 정도다. 공전속도의 1.55%에 불과하지만, 아주 무시할 만한 수준은 아니다.

[3] 지구 공전방향의 반대 방향으로 지구에서 멀어지는 우주선의 경우, 태양의 위치를 기준으로 본 우주선의 속도는 지구 공전속도에서 우주선이 지구에서 멀어지는 속도를 뺀 속도다.

[4] 공전궤도가 동그라미 모양이라는 가정을 했을 경우에 그렇다. 동그라미 모양에서 많이 벗어난 타원 모양이면 다른 계산이 필요하다.

[5] “우주탐사선, 행성공전 이용한 비행속도 증가 어떻게?”(윤복원, 한겨레 <사이언스온>, 2015년 10월14일.)

[6] 반드시 행성에 다가갈 필요는 없다. 위성의 중력을 이용해 중력도움 항법을 시행하기도 한다.

[7] The maths that made Voyager possible, Christopher Riley and Dallas Campbell, BBC 4, October 23, 2012. https://www.bbc.com/news/science-environment-20033940

[8] "Gravitational assist in celestial mechanics?a tutorial", James A. Van Allen, Am. J. Phys. 71, 448 (2003)